DC resistivity: measurements and data

Introduction

All geophysical surveys involve energizing the earth in order to generate signals, which will contain information about the types and distributions of subsurface physical properties.

For DC resistivity surveys, the energy source is a generator which injects a constant current into the ground using two electrodes. The "signals out" (data) are voltages measured at various places on the surface, along with strength of the known current source (in Amperes) and details about relative geometry of the four electrodes.

In order to create maps or graphs of raw data for quality assessment or for direct interpretations, measurements are converted into a form that is related to the relevant physical property. For each measurement, a 3D version of Ohm's Law is used to generate a datum with units of resistivity (or condutivity). These transformed data are called apparent resistivities because they represent the earth's true resistivity only if the ground is uniform within range of the measurement. When subsurface resistivity varies, interpretation must be based upon the way in which apparent resistivity varies as a function of electrode geometry and position. The commonly used survey procedures are explained later on this page, after discussions about current flow, sources, measurements, and conversion to apparent resistivities.

Current flow in the ground

The path of the current in the earth after it is injected with two electrodes depends upon the distribution of electrical resistivity. If the Earth is uniform, current flows in a regular three dimensional pattern under the electrodes as illustrated Figure 1. The north slice number 8 (flagged with a *) is similar to the type of image commonly shown in texts to indicate how current flows in two dimensions under a pair of source electrodes.

Figure 1. These figures show slices through a uniform Earth with current flowing out of the right-hand (near) electrode and back into the left-hand (far) electrode. A connecting red line substitudes for a real generator. Vectors with white dots for heads show the direction of current flow, while their colour indicates the strength (or current density) in units of Log10 Amperes per square metre (A/m2); so the maximum shown is Log10(J)=-3.33, or J=0.000468 A/m2.

Top slice 1 slice 2 slice 3 slice 4 slice 5 slice 6 slice 7 slice 8 slice 9 slice 10 slice 11 slice 12 slice 13 shell North slice 1 slice 2 slice 3 slice 4 slice 5 slice 6 slice 7 slice 8 * slice 9 slice 10 slice 11 slice 12 slice 13 slice 14 slice 15 slice 16 East slice 1 slice 2 slice 3 slice 4 slice 5 slice 6 slice 7 slice 8 slice 9 slice 10 slice 11 slice 12 slice 13 slice 14 slice 15 slice 16 There is no need to click: moving your mouse over the links simulates animations. Vector plots of current distribution were generated using 3D EM modeling code developed by the UBC Geophysical Inversion Facility.

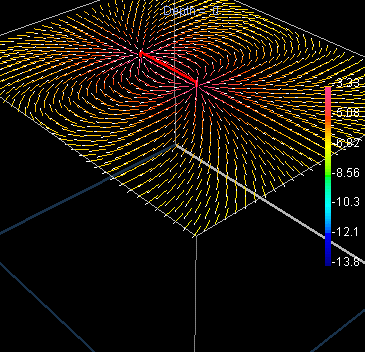Normally the earth is NOT uniform. Galvanic currents will flow towards regions of high conductivity and away from regions of high resistivity, as illustrated in Figure 2.

Figure 2. Click buttons for images a. through e.
a.		The Elura ore body. Depth to top of gossan (in blue) is approximately 100 m.
b.		A DC resistivity survey involves injecting current at one location and measuring resulting potentials at another location.
c.		Current will flow. Current density increases within conductive regions, and decreases within resistive regions.
d.		Charges build up at interfaces between regions of different electrical conductivity.
e.		Variations in charge distribution are detected as variations in distribution of potential, or voltage, at the surface.
			Elura Orebody Electrical resistivities Rock Type Ohm-m Overburden 12 Host rocks 200 Gossan 420 Mineralization (pyritic) 0.6 Mineralization (pyrrhotite) 0.6 Figure 2. The Elura orebody (in New South Wales, Australia) is an example of a subsurface target with a range of electrical resistivities. Details are from I.G. Hone, Geoelectric Properties of the Elura Prospect, Cobar, NSW, in "The Geophysics of the Elura Orebody, Cobar NSW," 1980, Australian Society of Exploration Geophysicists.

---

The relation between charge distribution, current flow and resulting potentials is discussed more fully in the section on principles.

Sources

High power and reliable constant current are the primary requirements of DC resistivity transmitters. For small scale work (electrodes up to roughly 100 m apart), a transmitter capable of sourcing up to several hundred milliwatts of power might be adequate. For larger scale work (electrodes as much as 1000 m or more apart), it is possible to obtain transmitters that can source up to 30,000 watts. See the appendix called "Instruments" for more details.

Current is usually injected as a 50% duty cycle reversing square wave (Figure 3). That is, current is on for several seconds, off for several seconds, on with reversed polarity, off, etc. Voltages are recorded while current is on.

Figure 3.

This pattern for the current source is necessary because a voltage measured when the current is off will be non-zero in many situations. Naturally occuring potentials are called spontaneous or self potentials (SP), and they are usually caused by electrochemical activity in the ground. From the point of view of DC resistivity surveys, SP voltages are noise because measured voltages must be caused by the source current only. The 50% duty cycle reversing square wave is employed so as to remove the (poorly known) SP signals.

Measurements: potential difference

It is tempting to compare the earth to a resistor in an electric circuit (Figure 4a). However, it is important to recognize the difference between resistance and resistivity. If we apply Ohm's law, R=V/I, to the situation in Figure 4b, we will have a resistance, which is in units of Ohms. This is NOT the ground's resistivity, which has units of Ohm-m. We do not want the resistance of this circuit; we want a measure of the ground's resistance per unit volume, or resistivity.

Figures 4.   a.      b.

In order to derive the relation between measurments (I, V, geometry) and the required physical property (resistivity or ) we should start from first principles. This is done in detail in the section called principles. The derivation is a three step process:

• First find a relation for potential due to a point source of current in a uniform medium with no boundaries (image to the right). The expression will look like Ohm's law with the addition of terms involving the distance between source and potential measurement location.
• Next, the potential due to two sources (actually, a source and a sink) is the superposition of potentials due to each one.
• Finally, since we must make potential measurements using two electrodes, an expression for potential difference can be derived as the difference between relations for potential at single electrodes.

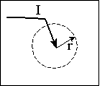
The actual measurement configuration can be summarized as shown in Figure 5. This conceptualization is useful, regardless of the actual placement of electrodes on the surface.

Figure 5.

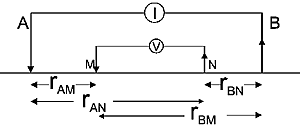
The measured voltage for any arrangement of electrodes can be derived from Figure 5 as follows (again, details are in the principles section):

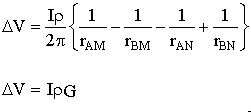
G is a geometric factor (including the factor 1/2), which depends upon the locations of electrodes.

Data: Apparent resistivity

We are finally in a position to express the thing we want (a physical property) in terms of parameters we either know or measure (current, voltage and geometry). Rearranging the last expression above, we can define apparent resistivity as the halfspace resistivity which produces the observed potential from a particular electrode geometry:

.  Similarily the apparent conductivity is .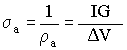

We have the following important definition: Apparent resistivity is the resistivity derived using only the known current, measured voltage, and array geometry. It is the earth's true resistivity only when the earth (within range of the measurements) is a uniform halfspace. When the earth is more complicated, the measured apparent resistivity will be less than the maximum and more than the minimum true (or intrinsic) resistivities that are within range.

The essence of interpreting resistivity surveys is to find the true distribution of intrinsic resistivities by interpreting the pattern of apparent resistivities that were measured.

Now we can find simple relations between all our known and measured quantities and a useful physical property, namely the apparent resistivity. We only need expressions for the geometric factor based upon electrode geometry. G is easily found if the four distances take on convenient values. For example, if electrodes are spaced equally by a distance a, then, using the figure and relation for V above,

G = (1/a - 1/2a - 1/2a + 1/a)/2 = 1/2 a.

This is the case for the "Wenner" array shown in Figure 6, which summariz    es the geometric factor for a variety of common electrode configurations. Note that in this figure, k=1/G . Usage of the various arrays is illustrated in the next section.

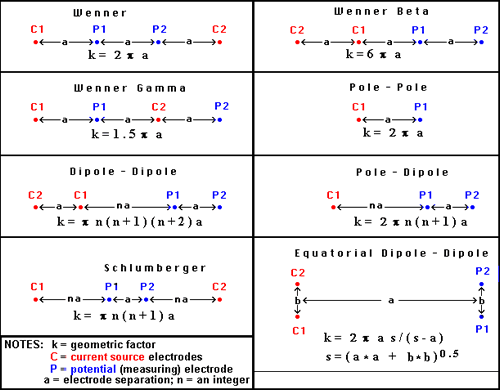
Figure 6. Survey configurations for DC resistivity surveying.

Survey configurations

There is a wide assortment of configurations commonly used for gathering DC resistivity (and induced polarization) data. In the field, the choice of array depends upon:

1. The type of information needed. For example, the location of a target may be all that is needed, or it may be necessary to characterize the details of the target.
2. The most likely type of model (1D, 2D, or 3D) that will be used for interpretation.
3. The economics of the situation. Since wires must be placed to all electrode locations, and electrodes must be planted in the ground, surveys covering large areas in difficult terrain with hard or gravelly surface materials can rapidly become very expensive.

The most common specific arrays are detailed in Figure 7, but there are several general types of surveys conducted on the surface.

Soundings provide 1D solutions, or vertical structure under one surface location. Electrode geometry is varied symmetrically about a single measurement location. The most common configurations for soundings are the Wenner and Schulmberger arrays.

Profiling provides information about lateral variations, usually with some information about vertical variations. Most profiles involve placing all electrodes on survey lines so that 2D models of the earth's electrical structure can be found. All seven types shown in the interactive figure below (Figure 7) can be used for profiling.

Three dimensional configurations of several types exist, in which electrodes are not in line. Examples include:

• Equatorial dipole-dipole array (Figure 6 above), which is used primarily for very shallow work such as archeological investigations.
• Twin Probe configuration (basically a Wenner Gamma in Figure 6 above, but with spacing more like dipole-dipole) is also used mainly for very shallow investigations such as archeological work.
• The so-called E-Scan technique is a pole-pole configuration. However, it is organized by planting a large number of electrodes all over the area of interest, without trying to stay on a grid or on lines. Potentials are recorded at all electrodes and one is used for a current source. Then a new electrode becomes a current source, and all potentials are recorded. Once an electrode has been used as a source, it is never used again. This large data set must be inverted in order to obtain interpretable information. The E-Scan technique is expensive but it has been used in the exploration for geothermal energy and minerals.
• Off-line profiling involves moving the sources along one survey line and recording potentials using electrodes planted along a different (usually parallel) line.
• There are also numerous other proprietary or experimental electrode configurations designed for 3D interpretation.

Azimuthal arrays are used to investigate the horizontal electrical anisotropy near the surface. Electrode configurations are usually one of the linear arrays (Wenner, dipole-dipole, etc.). However, instead of moving the array along a line (profiling), or expanding it about a central point (sounding), the array is rotated about a central point so that resistivity as a function of azimuthal direction can be plotted. Further details about the use of azimuthal arrays are given in an appendix III.

Borehole work often involves conceptually similar arrays with sources and receivers in various combinations of surface and down-hole locations. These are not discussed further here.

The following images show how electrodes are placed for the various named arrays. Electrodes placed on lines imply that the array is usually used for profiling. A circle at the array's centre implies that the array is generally expanded symmetrically about its centre for acquiring sounding data.

Figure 7. DC resistivity arrays a. dipole-dipole (dpdp) Most common profiling configuration. b. Several potential measurements are taken for each transmitter station. c. pole-dipole (pldp) Compared to dpdp, more efficient (move only one source electrode), deeper penetration, but lower spatial resolution. d. pole-pole (plpl) Compared to pldp, more efficient, deeper penetration, but lower spatial resolution. e. gradient array Poor depth information but rapid reconnaissance of large areas. f. Real section Potential electrodes move along lines between current source electrodes. g. Schlumberger sounding Distance "a" is on the order of one tenth of distance "b". h. For soundings, "b" can remain unchanged, as long as a << b, and measured potentials are strong enough to record. i. Wenner sounding The three spacings between electrodes are kept equal for all measurements. j. For soundings all electrodes must be moved for each new datum.

Plotting raw data

How are apparent resistivities (calculated from measured potentials, currents and geometries) displayed for direct interpretation or for quality assessment? There is one conventional plotting scheme for soundings, while plotting of profiles depends upon the survey configuration.

Soundings

Soundings are used when the earth's electrical structure needs to be interpreted in terms of layers under a single location at the surface. The electrode spacings are varied symmetrically about a central location.

Therefore, data must be plotted as a function of electrode spacing rather than as a function of location. The resulting plot is called a sounding curve, and it arises as shown in this interactive figure (Figure 8). Only current electrodes are shown. Potentials would be measured inside current electrodes using either the Wenner or Schulmberger configurations. At small electrode spacings current flows only in near-surface regions. Apparent resistivities look similar to the true resistivity of overburden. As current flows deeper, apparent resistivities are influenced by the true resistivities of deeper materials. The sounding curve begins to indicate that there are at least 2 layers under this location. At very large electrode spacings most of the information reflects deeper ground because that is where most of the current is flowing. The completed sounding curve. Figure 8.

Profiling

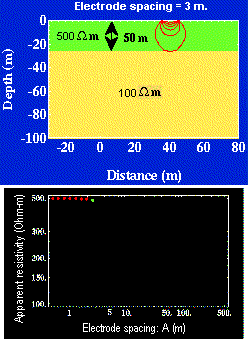Simple profiling involves moving a fixed array of four electrodes along a survey line. If there are no changes of spacing, then a simple graph of apparent resistivity versus line position would be adequate. A contour plot could be created if there is suitable coverage of the area.

Pseudosections: When profiling, potentials are usually measured at several positions for every current source location. Results at wider separations between the potential pair and the transmitter pair provide some information about deeper structures. The conventional method of plotting such results is the pseudosection, so called because it is not a true geological cross-section. Values of apparent resistivity are plotted on the graph as shown in Figures 9 and 10. The vertical axis represents separation distance, NOT depth. When all values are plotted, the result is contoured. Interpretation is tricky and requires some experience.

Figure 9. Plotting a pseudosection of dipole-dipole data: current electrodes are spaced a metres apart (same for potential electrodes), and current-voltage separation is n×a metres (n is an integer).

---

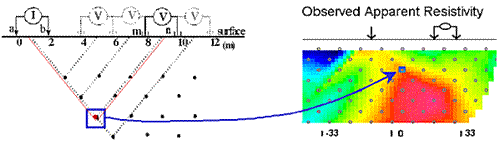
In the animation in Figure 10, the process of gathering and plotting profiling data is illustrated. The survey illustrated involves a dipole-dipole array with a = 2 metres, and n = 4.

Figure 10. For each measurement, notice the positions of current electrodes (left pair) and potential electrodes (right pair).  Vertical axis of the plotted data is NOT depth; it is the value n, from 1 to 4 in this case.    1. Display the finished contoured pseudosection.    2. Return to the animation.

Gradient array: Large scale reconnaissance surveys are sometimes done using the gradient array (Figure 7e above). If the current sources are not moved, then the energizing field is the same for all measurements. There is, therefore, no inherent information about variations with depth, just like the case of gravity and magnetic surveys. Gradient array surveys are often displayed simply by contour plotting the results.

Real Sections: There is one variation of the gradient array that provides limited information about structures at depth. It is run under the trade name "real-section," but the plot is still a "pseudosection" because apparent resistivity data are plotted with no attempt to convert apparent (measured) resistivities into true (intrinsic) resistivities. In the following figures, red electrodes are the current source, and blue electrodes are the potential measurement electrodes. A row of potential measurements at fixed "a" spacing is gathered for each pair of current electrode placements. This is basically a set of seven (in this case) gradient surveys along the same line. At four stages in acquisition, the data look like the following:

Figure 11. Although the result is not a "real" section at all, data can be inverted as for any other pseudosection to provide a more legitimate estimate of the true Earth resistivity structure. This example shows data gathered over the San Nicolas deposit in Mexico. 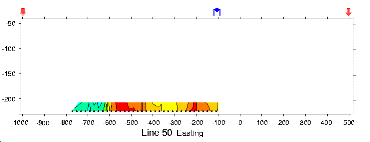After several measurements at one current source spacing. After changing to narrower current spacing and re-doing potential measurements. Over halfway completed. The completed "real-section" pseudosection.

Choice of array: Does the choice of array type matter for profiling? Appendix II has a brief comparison of pseudosections and the results of inverting data gathered using the arrays.

Processing options

Very little processing is applied to most raw resistivity data, other than to convert from apparent resistivities to potentials if that is needed for input to inversion programs. This is accomplished by using the apparent resistivity formula for the array in use, and the known geometric factor. If the current, I, is taken to be 1 (even if it was not 1 Amp in the field), then the result is a normalized potential in units of volts.

Interpretation of soundings and profiles

Interpretation of data is not part of this first version of the AGLO module on DC resistivity. Version 2 will explain current standard interpretation procedures.

For soundings, the earth is usually modeled as a sequence of layers. Forward modeling procedures are common and efficient. They involve estimating an initial simple model (a few layers) based on raw data, entering the estimated thicknesses and resistivities into a computer program that calculates data for the model, comparing these calculations to measurements, and adjusting the model until there is a good correspondance between calculated data and measured data. Some programs will perform parameteric inversion, in which the number of parameters is set (number of layers), and the code determines values for these parameters such that calculated and measured data are as similar as possible.

For profiling, pseudosections are rarely interpreted directly. 2D inversion schemes are used to estimate 2D models of the earth that have pre-determined characteristics. Most commonly, models consist of many rectangular cells of fixed size (often half the minimum electrode spacing). The codes perform non-linear optimization calculations to determine models that are both "smooth" (adjacent cells are as similar as possible) and are capable of generating a data set that is within pre-assigned error specifications on measured data.

More details will be provided in a subsequent version of this AGLO resource on DC resistivity surveying.