| |
There is often confusion regarding units in magnetics. This arises because
relations can be derived from either of two fundamental principles, and
the results yield different units. In the cgs and emu system of units,
 is derived from the concept of magnetic force due to magnetic poles.
The magnetizing field (or magnetic field
strength), is derived from the concept of magnetic force due to magnetic poles.
The magnetizing field (or magnetic field
strength),  , is defined as a force
on a unit pole, so it has units of dynes per unit pole, which are called
oersteds. In the SI system of units, magnetic field is defined in terms
of the consequence of current flowing in a loop. Then, , is defined as a force
on a unit pole, so it has units of dynes per unit pole, which are called
oersteds. In the SI system of units, magnetic field is defined in terms
of the consequence of current flowing in a loop. Then,  has units of amperes
per meters (which = 4 has units of amperes
per meters (which = 4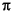 × 10-3
oersted). × 10-3
oersted).
Now, what if there is a magnetizable body in the presence of  ?
The body becomes magnetized due to the reorientation of atoms and molecules
so that their spins line up. The amount of magnetization, m, is
quantified as magnetic polarization, also known as magnetization
intensity or dipole moment per unit volume. The lineup
of internal dipoles produces a field, m, which,
within the body, is added to the magnetizing field. m has
units of ampere-meter2 per
meter3, which is amperes per metre, the same as ?
The body becomes magnetized due to the reorientation of atoms and molecules
so that their spins line up. The amount of magnetization, m, is
quantified as magnetic polarization, also known as magnetization
intensity or dipole moment per unit volume. The lineup
of internal dipoles produces a field, m, which,
within the body, is added to the magnetizing field. m has
units of ampere-meter2 per
meter3, which is amperes per metre, the same as  . .
In low magnetic fields, m is proportional to  ;
in fact, m = k ;
in fact, m = k ,
where k is magnetic susceptibility,
a physical property. k in the two systems of
units is related according to kSI=4 ,
where k is magnetic susceptibility,
a physical property. k in the two systems of
units is related according to kSI=4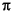 kemu. kemu.
The magnetic induction (or magnetic flux
density),  , is
the total field within the magnetic material, including the effect of magnetization. , is
the total field within the magnetic material, including the effect of magnetization.
 can
be written as: can
be written as:
 =
µo( =
µo( +
m) = (1 + k)µo +
m) = (1 + k)µo = µrµo = µrµo . .
The SI unit for  is
the tesla, which is 1 newton/ampere-meter. The cgs-emu unit for is
the tesla, which is 1 newton/ampere-meter. The cgs-emu unit for  is
the gauss, which equals 10-4 tesla. The
magnetic permeability of free space (considered a universal constant) is µo =
4 is
the gauss, which equals 10-4 tesla. The
magnetic permeability of free space (considered a universal constant) is µo =
4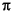 × 10-7 H/m (the
units are Henries/meter). The parameter µr is
the relative magnetic permeability, and its value is essentially 1 in
air or free space. The permeability, µ, is sometimes
used, and it is the quantity (1 + k)µo = µrµo = µ. × 10-7 H/m (the
units are Henries/meter). The parameter µr is
the relative magnetic permeability, and its value is essentially 1 in
air or free space. The permeability, µ, is sometimes
used, and it is the quantity (1 + k)µo = µrµo = µ.
The above relation shows how a material's magnetic permeability
relates to its magnetic susceptibility, k ,
and how the magnetic flux density within a material depends upon both the
ambient field and the induced magnetic moment. There can
be some confusion as to whether permeability, µ, or
the relative permeability, µr, is
being used, but you should be able to tell by the value. However, it is
best to check, if possible. Susceptibility is becoming the most commonly
used physical property for geophysical work, but use of permeability
can still be found in older work, or in some countries.
The tesla is
a large unit compared to the magnetic fluxes that we ordinarily deal
with in applied geophysics, so we generally use a subunit nanotesla (nT)
where 1 nT=10-9 T. There is also another unit,
the gamma, which
is numerically equivalent to the nT. That is, 1 nT = 1 gamma.
The strength of the earth's magnetic field varies between approximately
25,000 and 70,000 nT, depending upon latitude.
So, in the end, are we measuring  or or  during
geophysical surveys? This confusion stems partly from the fact that the
two are linearly related, so that a map of one looks exactly like a map
of the other, except for the units. Most geophysical magnetic surveys involve
measuring during
geophysical surveys? This confusion stems partly from the fact that the
two are linearly related, so that a map of one looks exactly like a map
of the other, except for the units. Most geophysical magnetic surveys involve
measuring  and
maps are shown in units of nanoteslas. If the maps and interpretations
are discussed in terms of and
maps are shown in units of nanoteslas. If the maps and interpretations
are discussed in terms of  ,
the conclusions will not change, so the distinction is not usually worried
about. ,
the conclusions will not change, so the distinction is not usually worried
about.
See also the  sidebar on
magnetic units, which discusses units in the context of the UBC-GIF dipole
JAVA applet., which in turn, is discussed more fully in the section
which discusses the response to buried dipoles . sidebar on
magnetic units, which discusses units in the context of the UBC-GIF dipole
JAVA applet., which in turn, is discussed more fully in the section
which discusses the response to buried dipoles .
|
|

