Travel Time Curves for Multiple Layers

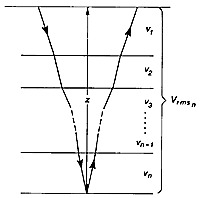
If there are additional layers then the seismic energy at each interface is refracted according to Snell's Law. The energy no longer travels in a straight line and hence the travel times are affected. It is observed that for small offsets, the travel time curve is still approximately hyperbolic, but the velocity, which controls the shape of the curve, is an "average" velocity determined from the velocities of all the layers above the reflector. The velocity is called the RMS (Root Mean Square) velocity, V_rms.  

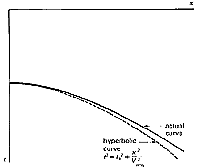(a) The complex travel path of a reflected ray through a multilayered ground. (b) The time--distance curve for reflected rays following the above type of path. Note that the divergence from the hyperbolic travel-time curve for a homogeneous overburden of velocity Vrms increases with offset.  From Kearey, Philip and Micheal Brooks, An Introduction to Geophysical Exploration. 2nd ed. Blackwell Science: 1991.

As outlined in the figure above, the reflection curve for small offsets is still like a hyperbola, but the associated velocity is  V_rms , not a true interval velocity.

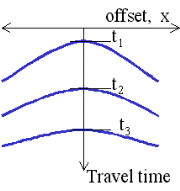
For each hyperbola,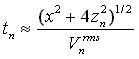

By fitting hyperbolas to each reflection event one can obtain (t_n,  V_n^rms) for n = 1, 2, ...  The interval velocity and layer thickness of each layer can be found using the formula below.
 

These formulae for the interval velocity and thickness of the n^th layer are directly obtainable from the definition of V_n^rms given above.
The RMS velocity for the n^th layer is given by,

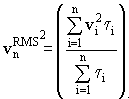
where v_i is the velocity of the i^th layer, and t_i is the one-way travel time through the i^th layer.