|
Seismic velocites and materials |
Relating geology to velocity
The relations between elastic properties and velocity, introduced under "Fundamentals", are given again here.
The two elastic constants and density each depend on the properties that geologists or engineers use to characterize the rock. These are the "secondary properties", including porosity, fluid saturation, texture etc. Many of these relationships are empirical – velocities are found to be related to certain rock units in a given locale by actual laboratory measurements on core samples of the rock or soil. One generally applicable rule is that seismic velocities generally increase with depth. However densities also increase with depth, so it must be that the bulk and shear modulii (K and u respectively) increase faster than the density. There are many empirical relationships between velocity and depth of burial and geologic age, and different publications will present these relationships in various graphical or tabular ways. In the next section, general expectations for how porosity, lithification, pressure and fluid saturation affect velocity are summarized. PorosityA very rough rule is the so called Wyllie's time average relationship (in which φ is the porosity):
This is not based on theory but is roughly right when the effective pressure is high and the rock is fully saturated. It is used extensively in the oil industry to convert data from "sonic logs" (which measure formation velocities directly) into porosity. Lithification (or cementation)The degree to which grains in a sedimentary rock are cemented together by post depositional, usually chemical, processes, has a strong effect on the values of elastic modulii. Also, by filling pore space with minerals of higher density than fluids, the bulk density is increased. The combination of porosity reduction and lithification contributes towards the observed increase of velocity with depth of burial and age. PressureCompressional wave velocity is strongly dependant on effective stress. For a rock buried in the earth, the confining pressure is the pressure of the overlying rock column, and the pore water pressure may be greater than, less than, or (if there is connected porosity to the surface) equal to the hydrostatic pressure. The effective pressure is the difference between the confining and pore pressure. In general velocity rises with increasing confining pressure and then levels off to a “terminal velocity” when the effective pressure is high. The effect is probably due to crack closure. At low effective pressure, cracks are open and easily closed with an increase in stress. This is the equivalent of saying there is large strain for low increase in stress, hence small K and low velocity. As the effective pressure increases the cracks are all closed, K goes up and the velocity increases. Finally even at depth, as the pore pressure increases above hydrostatic, the effective pressure decreases as does the velocity. Threfore, overpressured zones may be detectable in a sedimentary sequence by their anomalously low velocities. All this seems a bit complicated, and the take-home message is that there are several contributing factors to velocity, some of which may be counter-intuitive. Fluid saturationTheoretical and empirical studies have shown that the compressional wave velocity decreases with decreasing fluid saturation. As the fraction of gas in the pores increases, K and hence velocity decreases. Less intuitive is the fact that Vs also decreases with an increase in gas content. The reflection coefficient is strongly affected if one of the contacting media is gas saturated because the impedance is lowered by decreases in both the density and velocity. Velocity in unconsolidated near surface soils (the weathered layer)The effects of high porosity, less than 100% water saturation, lack of cementation, low effective pressure and the low bulk modulus (due to the ease with which native minerals can be rearranged under stress) combine to yield very low compressional and shear wave velocities in the weathered layer. Vp can be as low as 200 m/sec in the unsaturated zone (vadose zone) – which is less that the velocity of sound in air! AttenuationAttentuation is the reduction in amplitude (strength) of the seismic signal as it travels through the material. Seismic waves decrease in amplitude due to spherical spreading and due to mechanical or other loss mechanisms in the rock units that the wave passes through. The attenuation for a sinusoidal propagating wave is defined formally as the energy loss per cycle (wave length) Δ E/E where E is the energy content of the wave. There are many theories for explaining attenuation in rocks. Friction is a contributor, but does not explain laboratory measurement alone. Various other damping mechanisms such as viscous flow have more success but much important work remains to be done in this area, especially for unconsolidated material where the attenuation is very high. Some of the theories predict attenuation as well as dispersion (which means the variation of velocity with frequency). Experimentally it is found that attenuation depends on frequency, but velocity does not (much). Quantitatively, at one Hertz the amplitude decays by roughly two thirds in 10 km., whereas at 1000 Hz it decays by the same abount in 10 m. Also, attenuation may be as much as 10 times greater in unconsolidated sediments. Another important attenuation mechanism is the reduction in amplitude of a wave by the scattering of its energy by objects whose dimensions are on the order of the wavelength. For example, attenuation of a 1000 Herz signal in a shallow unconsolidated medium with a velocity of 250 m/sec can result in the signal being reduced to two thirds is original amplitued after travelling only 157 m. Therefore, it is reasonable to expect that the very high attenuation observed in near surface unconsolidated sediments is due to scattering. Energy at velocity boundaries
We define here the "Acoustic Impedance" Z = Transmission Coefficient: Note that at the interface there is continuity of displacement so that A0 = A1 + A2. Special Cases:
Remark: Large amplitudes of the transmitted wave are sometimes counter-intuitive. However, the energy transported in an acoustic wave is 
So even though there is an enhanced amplitude of a transmitted wave in certain situations, there is still loss of energy. The ratio of incoming to reflected energy is ER and the ration of incoming to transmitted energy is ET. The values of these rations are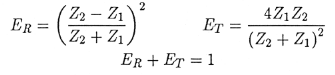 
|
The velocities of various rock types vary rather widely so it is usually difficult to determine rock type based only upon velocities. The table to the right shows rough ranges of velocities in units of kilometers per second for several types of earth materials. Therefore seismic surveys are most effective at delineating structure, .i.e boundaries where rock type changes.
and 
.
V, or the product of density and velocity. Energy is reflected and transmitted at the interface. We define next expressions which describe the efficiency of reflection and transmission; 
